Theory
What is a Language?
Every Language is defined by specifying four sets:
Alphabet
The most primitive building block of a language is its alphabet. An alphabet is a finite set of symbols. The alphabet for English consists of letters A to Z (both capital and small) as well as punctuation marks. The alphabet for a programming language includes characters A to Z, a to z, and other characters such as -, +, *, /, ‘, “, etc.
Words
Having defined the alphabet for a language, we can define the words of that language. Each word is a combination of symbols from the language’s alphabet. The set of words for a language can be finite or infinite. The set of words in English is finite while the set of words in a programming language, with identifiers with arbitrary length, is infinite.
Grammer
The grammar of a language is a set of rules determining how sentences in the language can be constructed.
The English grammar allows a sentence like “Olivia goes to work” while it rejects a sentence like “Oliva to home went” (although all words are in English).
The Go programming language allows a statement like var i int while it does allow a statement such as int i.
Semantic
The semantics of a language, also known as type system, determines which sentences are meaningful and which ones are not. In English, “Olivia eats an apple” makes sense while “An apple eats Olivia” does not! This is because in English an object with type human can eat an object with type fruit while an object with type fruit cannot eat an object with type human!
Different Types of Grammars and Languages
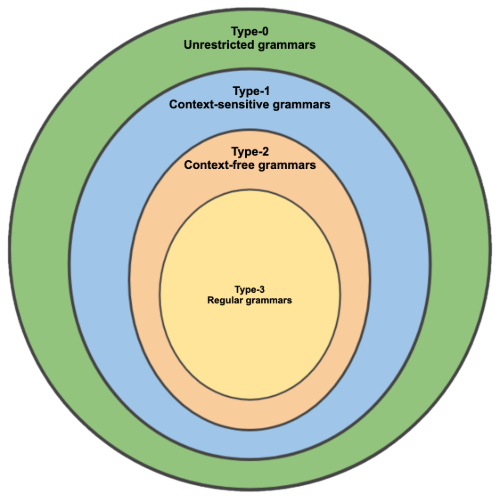
In the theory of formal languages, there are four types of grammars and respectively four types of languages. These classes of formal grammars have been formulated by Noam Chomsky in 1956.
Type-3
Type-3 grammars, also known as regular grammars, generate regular languages. These languages can be represented and decided by a finite state machine. In a finite state machine, the next state is the function of current state and the input. Equivalently, these languages can be denoted by regular expressions.
Type-2
Type-2 grammars, also known as context-free grammars, generate context-free languages. Type-2 grammars are a superset of type-3 languages. These languages can be represented and decided by a non-deterministic pushdown automaton. In a pushdown automaton, the next state is the function of current state, the input, and the top of the stack. Most programming languages are context-free languages (and its subset of deterministic context-free languages).
BNF (Backus normal form) is a notation for defining context-free grammars. We will also use this notation for defining the grammar for our language.
Type-1
Type-1 grammars, also known as context-sensitive grammars, generate context-sensitive languages. Type-1 grammars are a superset of type-2 languages (thus type-3 languages as well). These languages can be represented and decided by a linear bounded automaton.
Type-0
Type-0 grammars, also known as unrestricted grammars and recursively enumerable, contains all formal grammars. They generate all languages that can be represented and decided by a Turing machine.
What is a Compiler?
A compiler is a computer program that translates a source code written in one programming language (source language) into another programming language (target language). Compilers are usually used for translation from a higher-level programming language (Go, C/C++, etc.) to a lower-level one (assembly, binary code, etc.) for creating an executable program.
Compilers Architecture
Compilers benefit from a moduler design. Very high level, compilers have three modules: front-end, middle-end, and back-end.

Front-end
The front-end of a compiler takes the source code as input and generates an intermediate representation for it. The front-end has four sub-modules: lexer (scanner), parser, semantic analyzer, and intermediate code generator. Hence, lexers are usually implemented using finite state machines.

Lexer or scanner takes the source code as a stream of characters, tokenize them, and returns a stream of tokens as output. If you remember, a language is defined by four sets. Characters are defined by language alphabet and tokens are defined by language words. Tokens are language keywords, valid identifiers, literals, and so on. Tokens are defined using regular expressions (type-3).
The parser is the sub-module that understands the language grammar. The parser takes the stream of tokens and generates an abstract syntax tree. Abstract syntax tree is a data structure that has all sentences (expressions) of your program. The syntax of a language is usually defined using context-free grammars (type-2) and in BNF (Backus normal form).
The semantic analyzer is the sub-module that understands the language semantic. It traverses the AST (abstract syntax tree) and ensures sentences (expressions) are semantically valid using the type system. The output of this module is an intermediate representation which is the AST with additional metadata, properties, and resolved references using symbol table.
The front-end of a compiler is the core of a compiler. It translates the source code into a machine-independent code that can later be translated into machine-dependent code.
Middle-end
The middle-end of a compiler takes the raw intermediate representation and optimize it. The optimization is still independent of the target machine.

Back-end
The back-end of a compiler takes the (optimized) intermediate representation and generates a machine-dependent code that can be executed. It has two sub-modules. The first sub-module generates machine code and the second sub-module optimize the generated machine code. The end result is an assembly code targeted and optimized for a specific architecture (386, amd64, arm, arm64, …).

Tools
In this section, we briefly review some of the widely-used tools available for building compilers.
Lex/Flex
Lex is a program for generating and creating lexers and scanners. Flex (fast lexical analyzer generator) is an alternative to Lex. Flex takes an input file that defines all valid tokens (words) of a language and generates a lexer in C/C++. You can find an example of using Flex here.
Yacc/Bison
Yacc (Yet Another Compiler-Compiler) is a program for creating and generating LALR parsers (Look-Ahead LR parser). Bison is a version of Yacc. Yacc/Bison are used together with Lex/Flex. Bison reads a specification of a context-free language written in BNF and generates a parser in C/C++. You can find an example of using Bison here.
LLVM
LLVM (The LLVM Compiler Infrastructure) is an open-source project providing a set of tools for building a front-end for any programming language and a back-end for any target instruction-set (architecture). LLVM is built around a machine-independent intermediate representation which is a portable high-level assembly language. You can find the examples and tutorials here.
Building A Compiler in Go
Now it is time for the fun part! We want to build a micro-compiler in Go.
Our language is a logical formula of labels with ANDs and ORs.
For example, ((sport,soccer);(music,dance)) means we want all contents either related to sport and soccer or related to music and dance.
Our compiler is going to create a SQL query for a given label formula.
You can find the source code for this example here
Defining The Language
Let’s first define our language.
Our language has a very simple syntax for defining a logical formula of labels for querying different contents.
For example (food,health) means that we want all products belonging to food and health categories.
Or, (store-1;store-2) means that we are interested in all products that are available either in store 1 or store 2.
For defining a language, we need to specify four sets: alphabet, words, grammer, and semantic. We define these four sets informally as follows:
- alphabet =
unicode characters,digits,-,,,;,(, and) - words =
(,),,,;, and<labels>(a unicode char followed by unicode chars, digits, or/and -) - grammar = a sequence of
<labels>separated by,or;and enclosed by(and) - semantic =
empty set(no semantic and no type-system)
Examples of letters in the alphabet are a, b, c, m, x, 0, 1, 7, -, (, ).
Examples of words are food, health, store-1, store-2, (, ).
Examples of sentences (based on words and grammar) are (food,health), (store-1;store-2).
Building The Compiler
For building a compiler, we need to build a scanner and a parser. The parser will create the abstract syntax tree (intermediate representation). We then use AST to generate our target code.
goyacc is a version of Yacc for building parsers and syntax analyzers in Go.
For building the scanner in Go, there is no equivalent of Lex. You have a few options.
Depending on how complex is your language, you can create your own scanner/lexer using available packages such as text/scanner.
There are also tools like Ragel for generating lexical analyzers in Go.
Many times, using a tool for generating your lexer is overkill and generated lexers are not usually as fast as hand-written ones.
Parser
We first start by formally defining our language grammar (syntax) and creating a parser for it.
Here is our language grammer in in BNF (Backus normal form):
formula ----> '(' expr ')'
expr ----> label | '(' expr ')' | expr ',' expr | expr ';' expr
Our grammar has four rules.
This grammar is ambiguous in the sense that precedence of operators (, and ;) are not specified,
and we don’t know if we should group operands of these operators from the right or the left (associativity).
We show these ambiguities using an example:
- Grouping
l1;l2;l3;l4- Left –>
((l1;l2);l3);l4) - Right –>
(l1;(l2;(l3;l4)))
- Left –>
- Precedence
l1,l2;l3,l4,over;–>(l1,l2);(l3,l4);over,–>l1,(l2;l3),l4
To address these ambiguities, we give , and ; equal precedence and group them from left to right.
Here is our language grammar in Yacc (parser.y):
%{
package goyacc
func setResult(l yyLexer, root *node) {
l.(*lexer).ast = &ast{
root: root,
}
}
%}
%token OPEN
%token CLOSE
%token <op> OP
%token <label> LABEL
%type <node> formula
%type <node> expr
%left OP
%start formula
%union{
op string
label string
node *node
}
%%
formula:
OPEN expr CLOSE {
setResult(yylex, $2)
}
expr:
LABEL {
$$ = &node{typ: label, val: $1}
}
| OPEN expr CLOSE {
$$ = $2
}
| expr OP expr {
$$ = &node{typ: op, val: $2, left: $1, right: $3}
}
Let’s debunk our grammar.
%{
package goyacc
func setResult(l yyLexer, root *node) {
l.(*lexer).ast = &ast{
root: root,
}
}
%}
Whatever defined between %{ and %} will be inserted to the generated source code.
In this case, we are specifying our package name and adding a helper function to create an abstract syntax tree.
Next, we define our tokens and types:
%token OPEN
%token CLOSE
%token <op> OP
%token <label> LABEL
%type <node> formula
%type <node> expr
In our language, we have four types of tokens: OPEN, CLOSE, OP, and LABEL.
Notice , and ; are defined as one token (OP).
OPis tagged with <op> and LABEL is tagged with <label>.
These tags are correspondent to union fields that we will see shortly.
We also have two types: formula and expr.
Types are non-terminal (non-leaf) nodes in our abstract syntax tree.
When types are present, type-checking is performed.
Then, we specify associativities and precedences for our grammar constructs:
%left OP
In this case, our operators (, and ;) have equal precedence and they are left-associative.
Next, we specify the start symbol:
%start formula
formula is a non-terminal and the root of our abstract syntax tree.
When our parser reads the stream of tokens: TODO:
- For each token (terminals or leaves in AST), the value of the token (lexeme) needs to be returned.
- For each grammar rule (non-terminals in AST), a node needs to be returned.
We specify these values using a construct called union (In C/C++ the generated code will be a union and in Go it will be a struct).
%union{
op string
label string
node *node
}
Here, op and label are terminals or leaves in our abstract syntax tree.
Notice that we don’t have any terminal or leaf for OPEN and CLOSE tokens.
They are only used for specifying associativity and precedence to create the abstract syntax tree in a deterministic non-ambiguous fashion.
They are implied in the structure of the abstract syntax tree.
If you remember, OP token is tagged with <op>.
When our lexer reads an OP token, it sets the op field of the union to the actual value of token (, or ; lexeme).
Similarly, when our lexer reads a LABEL token, it sets the label field of the union to the actual value of the token (lexeme).
Using these tags, we are telling the parser where to find the actual values of tokens.
OPEN and CLOSE are tagged because we know OPEN always means ( and CLOSE always means ).
node is the type for non-terminal nodes in our abstract syntax tree.
Later, we define the node struct in our lexer as follows:
type node struct {
typ nodeType
val string
left, right *node
}
Each node is either a terminal (leaf) with value (val) or a non-terminal operator with left and right operands.
Finally, we define our language grammar in BNF after %%:
formula:
OPEN expr CLOSE {
setResult(yylex, $2)
}
expr:
LABEL {
$$ = &node{typ: label, val: $1}
}
| OPEN expr CLOSE {
$$ = $2
}
| expr OP expr {
$$ = &node{typ: op, val: $2, left: $1, right: $3}
}
Upon evaluation of each rule (non-terminals), we need to return a node type.
The node that has to be returned is defined between { and } after each rule.
When parser sees expr --> expr OP expr rule, we return the following node:
$$ = &node{
typ: op,
val: $2,
left: $1,
right: $3,
}
$$ is the variable that we are supposed to set the result on it.
op is a constant we define in our code.
$1, $2, and $3 are the values for tokens and types in the right side of rule (values for expr, OP and expr respectively).
Since formula is marked as %start, when we see the formula --> OPEN expr CLOSE rule, we need to complete our AST.
We do this by calling setResult function. yylex is the lexer we pass to the parser.
Now, we can generate the source code for our parser by running the following command:
goyacc -l -o parser.go parser.y
Now, let’s take a look at the generated file (parser.go).
The following function is what we are interested in:
func yyParse(yylex yyLexer) int {
...
}
This function receives an input parameter of type yyLexer which is an interface defined as:
type yyLexer interface {
Lex(lval *yySymType) int
Error(s string)
}
Now, we know what methods our lexer should implement (Lex and Error).
The parser will pass an input parameter of type *yySymType to Lex method.
yySymType is a struct defined as:
type yySymType struct {
yys int
op string
label string
node *node
}
You can notice that this struct is generated based on the union construct we defined in our parser.y.
Lexer
Here is the source code for our lexer (lexer.go):
//go:generate goyacc -l -o parser.go parser.y
package goyacc
import (
"errors"
"io"
"text/scanner"
"unicode"
)
type nodeType int
const (
op nodeType = iota + 1
label
)
const (
orOp = "OR"
andOp = "AND"
)
// node represents a node in abstract syntax tree
type node struct {
typ nodeType
val string
left, right *node
}
// ast is the abstract syntax tree for a label formula
type ast struct {
root *node
}
func parse(name string, src io.Reader) (*ast, error) {
l := newLexer(name, src)
yyParse(l) // generated by goyacc
return l.ast, l.err
}
// lexer implements yyLexer interface for the parser generated by goyacc
type lexer struct {
s scanner.Scanner
err error
ast *ast
}
func newLexer(name string, src io.Reader) *lexer {
var s scanner.Scanner
s.Init(src)
s.Filename = name
// Accept tokens with "-"
s.IsIdentRune = func(ch rune, i int) bool {
return unicode.IsLetter(ch) || unicode.IsDigit(ch) && i > 0 || ch == '-' && i > 0
}
return &lexer{
s: s,
}
}
func (l *lexer) Error(msg string) {
l.err = errors.New(msg)
}
// yySymType is generated by goyacc
func (l *lexer) Lex(lval *yySymType) int {
if token := l.s.Scan(); token == scanner.EOF {
return -1
}
lexeme := l.s.TokenText()
switch lexeme {
case "(":
return OPEN // generated by goyacc
case ")":
return CLOSE // generated by goyacc
case ",":
lval.op = andOp
return OP // generated by goyacc
case ";":
lval.op = orOp
return OP // generated by goyacc
default:
lval.label = lexeme
return LABEL // generated by goyacc
}
}
The code for lexer makes things more clear, but let’s go through a few important things.
The constants we used to return a node upon evaluation of a rule are defined here as:
const (
op nodeType = iota + 1
label
)
The values of OP are defined as:
const (
orOp = "OR"
andOp = "AND"
)
As we already see, node is defined as:
type node struct {
typ nodeType
val string
left, right *node
}
We are using the built-in text/scanner package for tokenizing and creating our lexer.
A Scanner by default skips all white spaces and recognizes all identifiers as defined by the Go language specification.
In our language, labels can have - between characters and digits.
We need to change the default behavior of Scanner, so it can recognize our labels properly.
We do this by defining a custom fucntion called IsIdentRune as follows:
s.IsIdentRune = func(ch rune, i int) bool {
return unicode.IsLetter(ch) || unicode.IsDigit(ch) && i > 0 || ch == '-' && i > 0
}
Here we say a character (rune) is part of our label if
- It’s a letter
- It’s a digit and it’s not the first character in the identifier
- It’s a hyphen and it’s not the first character in the identifier
Lex is called by yyParse() function and an input parameter of type *yySymType is passed to it every time (lval).
yySymType is generated using our union definition.
Using our scanner, we scan an identifier and then we figure out which type of token is that.
If the token is an OP, we set a value (either orOp or andOp) for it to op field of lval (we tagged OP token with <op>).
Likewise, if the token is a LABEL, we set its value to label field of lval (we tagged LABEL token with <label>).
Backend
Our compiler backend traverses an AST (abstract syntax tree) and creates a SQL query. Here is the source code for our compiler backend:
package goyacc
import (
"fmt"
"strings"
)
var opToANDOR = map[string]string{
orOp: "OR",
andOp: "AND",
}
// Formula represents a formula for labels
type Formula struct {
ast *ast
}
// FromString creates a new instance of formula from a string
func FromString(str string) (*Formula, error) {
src := strings.NewReader(str)
ast, err := parse("formula", src)
if err != nil {
return nil, err
}
return &Formula{
ast: ast,
}, nil
}
// postgresQuery traverses an AST in an LRV fashion and creates a SQL query
func postgresQuery(n *node, table, field string) string {
// Label (leaf node)
if n.typ == label {
return fmt.Sprintf(`EXISTS (SELECT 1 FROM %s WHERE %s LIKE '%%%s%%')`, table, field, n.val)
}
// Op node
if n.typ == op {
leftQuery := postgresQuery(n.left, table, field)
rightQuery := postgresQuery(n.right, table, field)
return fmt.Sprintf(`(%s %s %s)`, leftQuery, opToANDOR[n.val], rightQuery)
}
return ""
}
// PostgresQuery constructs a PostgreSQL query for the formula
func (f *Formula) PostgresQuery(table, field string) string {
where := postgresQuery(f.ast.root, table, field)
query := fmt.Sprintf(`SELECT * FROM %s WHERE (%s)`, table, where)
return query
}
The code is pretty straightforward. We traverse the abstract syntax tree recursively and construct the SQL query.
Running Tests
You need to first install goyacc. You can install it using go get command as follows:
go get -u golang.org/x/tools/cmd/goyacc
Then you need to generate parser.go from parser.y as follows:
go generate
Now, you run the tests or import your compiler from this package.
Conclusion
Compilers are an integral part of our experience as developers. They translate a program written in one language into another. A programming language is defined by specifying four sets: alphabet, words, syntax, semantic.
A compiler has three parts: front-end, middle-end, and back-end. The front-end translates source code into a machine-independent intermediate representation (IR). The middle-end optimizes the machine-independent intermediate representation. The back-end translates the machine-independent intermediate representation into a machine-dependent executable code. This modular design of compilers allows compilers developers to build their front-end independent of middle-end and back-end.